Exercitiul de clasa a II-a care a pus in dificultate mii de internauti. Care este raspunsul corect?

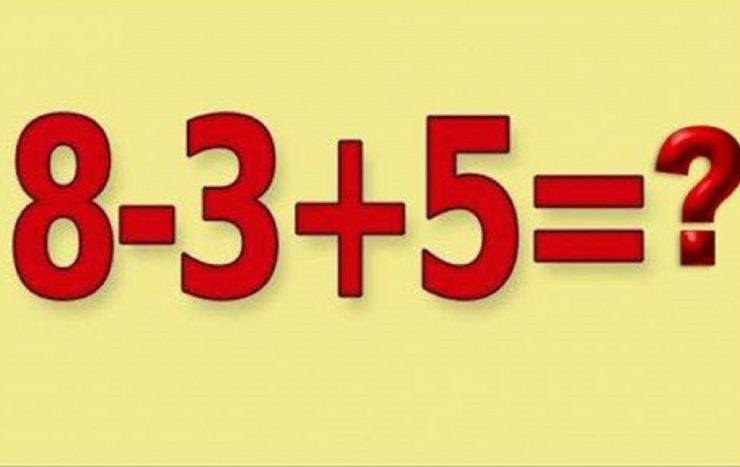
Un exercițiu simplu de matematică de clasa a II-a a reușit să pună în încurcătură mii de internauți care au încercat să-i dea de cap. Este vorba despre calculul 8 – 3 + 5, aparent banal, dar care a stârnit controverse din cauza aplicării greșite a regulilor matematice de bază.

Exercițiul care i-a încurcat pe mulți

Pentru cei care au răspuns „10”, felicitările sunt în ordine. Justificarea este simplă: atunci când într-o expresie matematică apar doar operații de același ordin, cum sunt adunarea și scăderea, acestea se efectuează în ordinea în care sunt scrise, de la stânga la dreapta. Astfel, 8 – 3 + 5 înseamnă: 8 minus 3, adică 5, plus 5, rezultând 10.

„Dacă ai răspuns 10, ești inteligent! Explicația: Dacă în exercițiu apar operații de același ordin (numai adunări și/sau scăderi, sau numai înmulțiri și/sau împărțiri), le efectuăm în ordinea în care sunt scrise. Așadar 8 – 3 + 5 = 10!”

De fapt, mulți uită cum funcționează succesiunea operațiilor în matematică. Acestea trebuie efectuate într-o ordine clară, stabilită încă din clasele primare, care spune următoarele:

• Operațiile din paranteze sunt întotdeauna prioritare. Dacă există mai multe tipuri de paranteze (rotunde, pătrate, acolade), se încep cu cele rotunde.
• Urmează operațiile cu un singur operator, cum ar fi factorialul.
• Se efectuează apoi ridicarea la putere și extragerea radicalului, iar în cazul puterilor compuse, calculul se face de sus în jos.
• În continuare, se trece la înmulțiri și împărțiri, în ordinea în care apar.
• Abia la final se rezolvă adunările și scăderile, tot în ordinea scrisă, de la stânga la dreapta.

Un exemplu concret este:
(4+10/2)/9 = [4+(10/2)]/9 = [4+5]/9 = 9/9 = 1.

Sau, în cazul expresiilor cu mai mulți pași:
232 = 29 = 512.

Elevii încep să învețe aceste noțiuni esențiale din clasa a IV-a, unde li se explică diferența între operațiile de ordinul întâi (adunare și scădere) și cele de ordinul doi (înmulțire și împărțire).

Atunci când într-un exercițiu apar doar operații de același ordin – fie adunări și scăderi, fie înmulțiri și împărțiri – regula este clară: le rezolvăm exact așa cum sunt scrise, de la stânga la dreapta. De exemplu:

• Exemplul 1. 9 + 4 – 5 = 13 – 5 = 8.
• Exemplul 2. 3 x 6 : 9 = 18 : 9 = 2.

Situația se complică atunci când în aceeași expresie se amestecă operații de ambele tipuri. În acest caz, începem cu cele de ordinul doi – înmulțirea și împărțirea – apoi trecem la cele de ordinul întâi – adunarea și scăderea. Iată câteva exemple care ilustrează clar această regulă:

• Exemplul 3. 7 – 7 : 7 = 7 – 1 = 6.
• Exemplul 4. 8 + 8 x 8 = 8 + 64 = 72.
• Exemplul 5. 7 x 6 – 3 x 10 + 18 : 9 = 42 – 30 + 2 = 12 + 2 = 14.

În acest ultim caz, ordinea a fost următoarea:

• 7 x 6 = 42
• 3 x 10 = 30
• 18 : 9 = 2
• 42 – 30 = 12
• 12 + 2 = 14

Aceste exemple arată cât de importantă este respectarea succesiunii corecte a operațiilor, chiar și în cele mai simple exerciții.

Pentru un copil de clasa a II-a, exercițiul 8 – 3 + 5 poate părea ușor, dar pentru un adult care n-a mai pus mâna pe un manual de matematică de zeci de ani, poate fi o adevărată capcană.

Reamintirea acestor reguli simple, dar esențiale, se dovedește utilă nu doar în școală, ci și în viața de zi cu zi, acolo unde logica matematică se aplică mai des decât am crede.